预备知识：微积分，线性代数，概率论，python(numpy, matplolib)

机器学习在我本科的毕业设计中有用到，不过当时只是浅浅地了解一下，现在补回来，感觉李老师的课还是很好理解的，先看主线，作业和选修那些后面再看。

---

1、什么是机器学习

machine learning (ML)≈ looking for function（找一个函数）

有数据有标签的*监督学习supervised learning* **

只有数据没有标签的无监督学习unsupervised learning

从经验中总结提升的强化学习reinforcement learning

和强化学习类似的，适者生存不适者淘汰的遗传算法genetic algorithm

Regression：回归，给输入，给予预测值

Classification：分类器，做选择题

Structred Learning：产生一些有结构的物件（图片、文件等）

1.1机器学习的一般步骤

（1）建立含有未知数的函数f(x)

模型model 特征feature 权重weight 偏差bias

$$
y = b + wx_1 \label{pythagorean}
$$

（2）从训练数据中定义损失函数Loss
$$
L(b,w) = \frac{1}{N} \sum e_n
$$

L越小，代表这一组参数(b,w)越好

其中e为真实值与预测值之差的绝对值 $e = \left | y - \hat{y} \right |$，L是平均绝对误差mean absolute error(MAE)。而以下这个，$e=(y-\hat{y})^2$，L是平均平方误差mean square error(MSE)

（3）最佳化Optimization

​ ①梯度差分

​ 找一组(w,b)，让Loss函数值最小，就是我们要找的参数w，b，用公式表示就是：
$$
w^*,b^*=arg\ \underset{w,b}{min}\ L
$$

​ 首先随机选取初始的值$w^0 \ & \ b^0$，计算偏导数
$$
\frac{\partial L}{\partial w}|{w=w^0,b=b^0} \
\frac{\partial L}{\partial b}|{w=w^0,b=b^0}
$$

​ 迭代地更新w和b，寻找偏导数为零的点$w$
$$
w_1 = w_0 - \eta\ \frac{\partial L}{\partial w}|{w=w^0,b=b^0} \
b_1 = b_0 - \eta\ \frac{\partial L}{\partial b}|{w=w^0,b=b^0}
$$
​ 其中$\eta$被称为学习率，即learning rate

缺点：可能只是找到局部最优解，而没有找到全局最优解（不是最难解决的问题）

注：以上3步建立的模型是线性模型，有很大的局限性。

1.2深度学习简介

深度学习时基于机器学习的概念及框架提出的，回到机器学习的框架：

(1)含有未知数的函数

①Sigmoid Function：S型函数

$$y = c \ \frac{1}{1+e^{-(b+wx_1)}} = c \ sigmoid(b+wx_1)$$

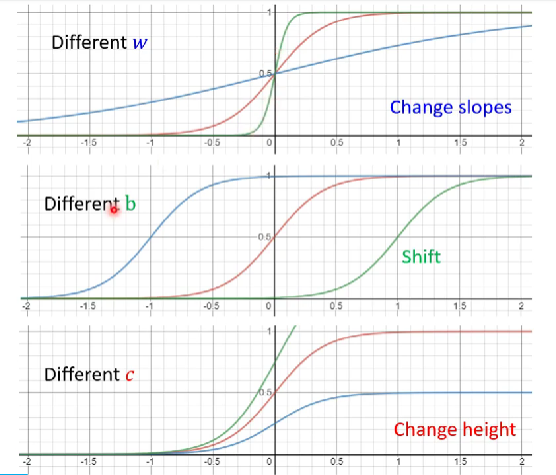
• 不同的w改变sigmoid函数的斜度
• 不同的b改变sigmoid函数的平滑度
• 不同的c改变sigmoid函数的高度

②RELU函数

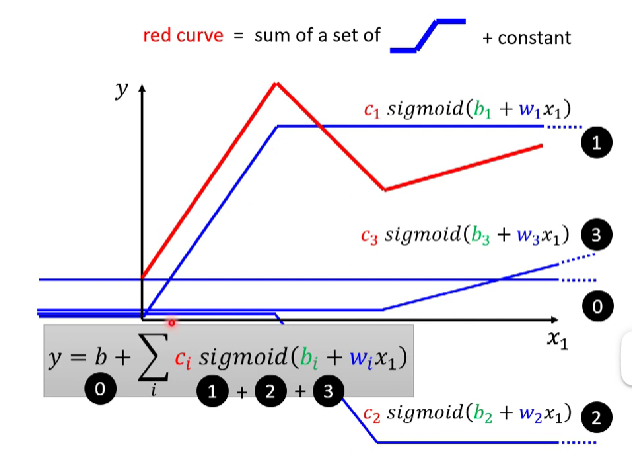其实RELU函数是很多个函数合成而来的，其中包含有sigmoid函数和常量函数。

​ 由上述可以推导出的新的模型：多特征模型

​ 假设有三个输入：$x_1,x_2,x_3$，分别乘上$w_{11},w_{12},w_{13}$以后相加，所得的和与$b_1$相加，此部分即为$r_1$，经过sigmoid以后输出$a_1$；改变权重对$x_1,x_2,x_3$重复上述操作，得到$a_2$、$a_3$，将他们分别和$c_1,c_2,c_3$相乘以后，相加，最后加一个b，就可以得到输出y了。（还不懂的结合矩阵小节的图）
$$
\begin{aligned}
{y}
& = b\ +\ \sum\limits_{i}\ c_i\ sigmoid(b\ +\ w_ix_1) \
& = b\ +\ \sum\limits_j\ w_jx_j \
& = b\ + \sum\limits_{i}\ c_i\ sigmoid\ (b_i\ +\ \sum\limits_jw_{ij}x_j)
\end{aligned}
$$

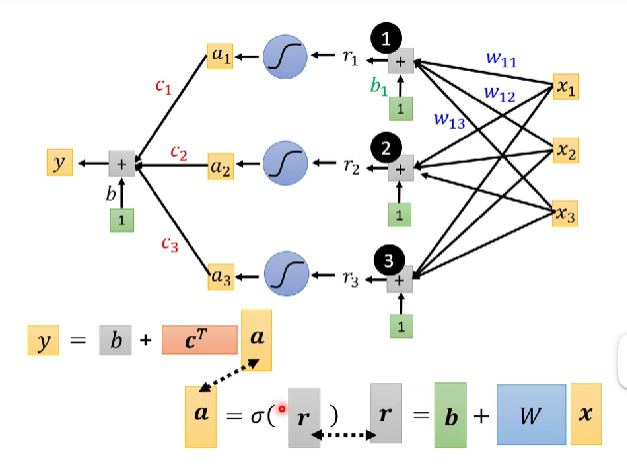
③矩阵形式的函数理解

​ 上述推导多特征模型的步骤中可见，有重复的步骤。那么从线性代数的角度来写岂不是简单很多！下图的上半部分是上面推导过程的图解部分，结合起来理解还是好理解的。颜色层代表的是矩阵的形状。

​ 把输入$x_1,x_2,x_3$拼成一个3×1的向量，$\vec{W}$是由$w_{ij}$拼成的3×3的矩阵，同理$\vec{b},\vec{r},\vec{a},\vec{c^T}$也是拼起来的。

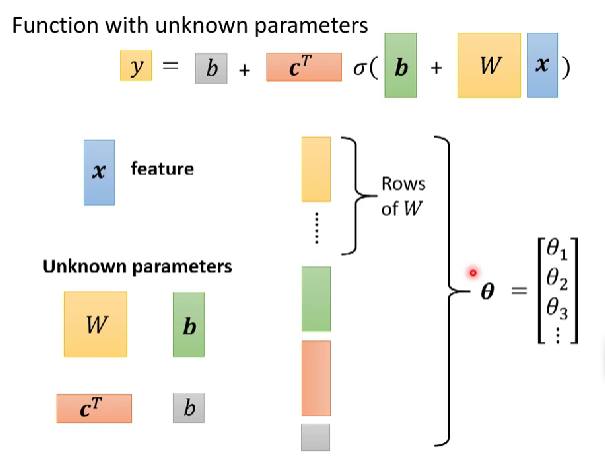
以上矩阵中，除了x是输入以外，其他的都是未知的参数，把他们拉长展成一列得到一个向量$\vec{\theta}$，其中的每一个元素用$\theta_i$表示。

\par\par

Q：Sigmoid Function可以不止3个吗？

A：可以，越多的Sigmoid Function，就可以逼近越复杂的Function。

\par\par

Q：可以直接写出Function，而不用逼近的方法吗？

A：首先他的Function直接写出来可能会比较复杂，较难写出来。如果可以写出来，也可以用Hard Sigmoid。完全有别的做法。

（2）从训练数据中定义损失函数Loss

Loss是有关参数的函数 *L(θ)*，Loss是衡量预测值与真实值之间的差异程度。

（3）Optimization优化

对于多特征函数里的未知量$\vec{\theta}$，当使得$\vec{L}$最小时，就是最优解。注意检验是否是全局最优解。$$\boldsymbol{\theta^*}=\arg\ \underset{\theta}{min}L$$

随机选取初始值$\boldsymbol\theta^0$
计算梯度$\boldsymbol{g}=\nabla L(\boldsymbol{\theta^0}) \ \boldsymbol{\theta^1} \leftarrow \boldsymbol{\theta^0}-\eta \boldsymbol{g}$

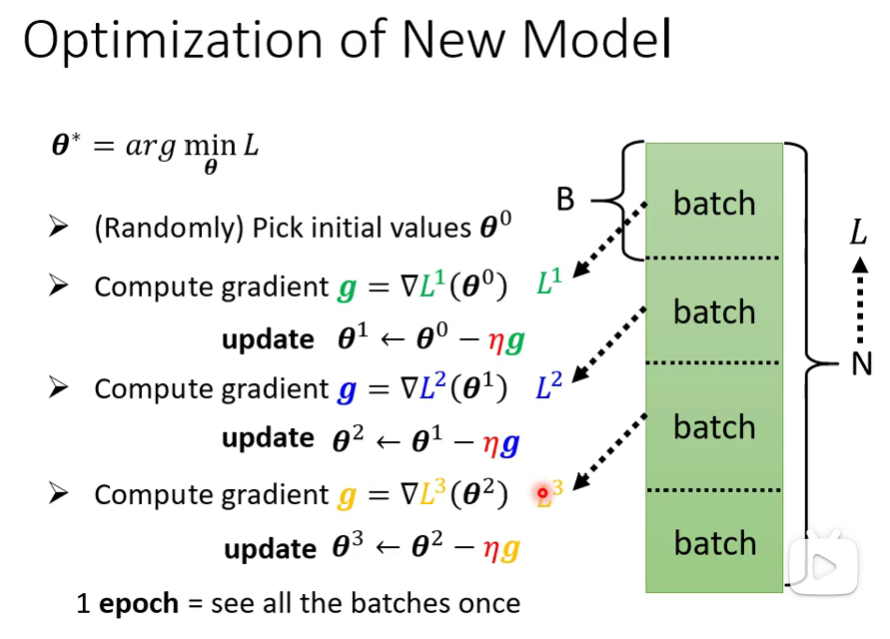每个batch里面有B个资料，每个batch的大小随机分就可以了，资料的数目可以不同，每个batch可以算出一个L，由第一个batch算出$L_1$，update一次参数；由第二个batch算出$L_2$，继续update一次参数……最后把所有的batch都看完就称为一个epoch。

Sigmoid ➡Rectified Linear Unit（ReLU）
$$
y = b\ + \sum\limits_{i}\ c_i\ sigmoid\ (b_i\ +\ \sum\limits_jw_{ij}x_j) \
y = b\ + \sum\limits_{2i}\ c_i\ max(0,b_i+\sum\limits{j}{w_{ij}}{x_ j})
$$
一个Sigmoid就可以表示一个Hard Function，但是两个ReLU才能合成一个Hard Function，所以是2i。
以上式子都统称为ActivationFunction激活函数

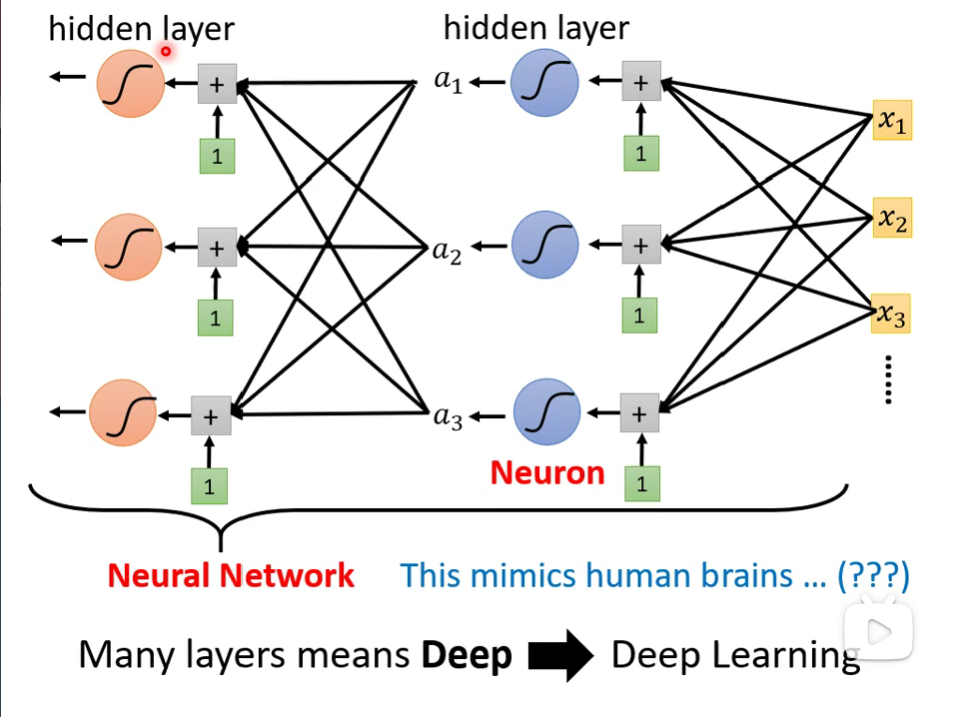
神经元到神经网络，但是现在已经不讲神经网络了，现在说的是层，层层组合，所以称之为深度学习。

过拟合（Overfitting）：在训练集上表现好，但在验证集上表现差。

__HyperParameter超参数__：自己设置的东西，而不是机器算出来的。
超参数：batch size、sigmoid函数的数量、learning rate