最近在准备秋招的事，笔试的时候遇到了动态规划，之前没学过，故来补档。笔试寄了啊！

定义

动态规划（Dynamic Programming，简称DP）是一种在计算机科学和数学中用于解决最优化问题的方法。它的基本思想是将一个复杂的问题分解成若干个相互重叠的子问题，并通过存储子问题的解来避免重复计算，从而达到提高效率的目的。

动态规划适用于满足以下两个条件的问题：

1. 最优子结构：问题的整体最优解可以通过其子问题的最优解构造得出。
2. 重叠子问题：在使用递归算法自顶向下求解问题的过程中，每个子问题被重复计算多次。而动态规划通过记录已解决的子问题的答案来避免重复计算。

动态规划可以采用两种方法实现：

• 自底向上（Bottom-up）：从最小的子问题开始求解，逐步构建更大的子问题的解，最终得到原问题的解。这种方法通常使用数组或表格来存储中间结果。
• 自顶向下（Top-down）：也称为带备忘录的递归（Memoization），先尝试求解原问题，遇到已经解决过的子问题则直接返回之前的结果，否则递归求解该子问题并存储结果。

动态规划可以用来解决很多经典问题，例如背包问题、最长公共子序列问题、最短路径问题等。

实例1

题目

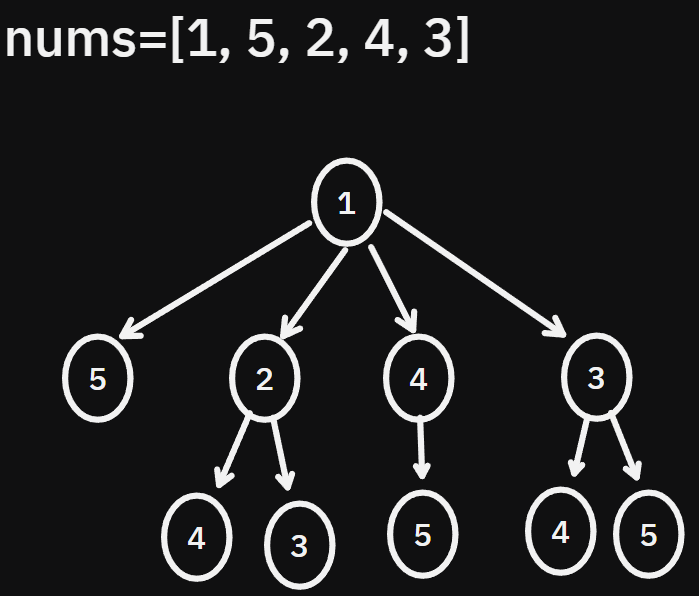
给定无序数组nums=[1, 5, 2, 4, 3]，找出其中最长的递增子序列，返回最长递增子序列的长度。

思路

在初始尚未接触动态规划前，想到的办法是暴力枚举/暴力搜索。

• 假如我们第一个数字选’1’，那么我们第二个数字可以选’5’，’4’，’3’，’2’；
  • 假如我们第二个数字选’5’，那么没有其他比’5’大，此时序列长度为2；
  • 假如我们第二个数字选’2’，那么下一个数字可以选’4’或者’3’，此时序列长度为3；
  • … …依次类推
• 最后统计从第二个数字的各种可能性的序列长度
• 选出最长的那个，算法结束

代码实现

def L(nums, i)
	"""返回从第i个数字开始的最长子序列长度"""
    
    if i == len(nums) - 1:	# 最后一个数字
        return 1
    
    max_len = 1
    for j in range(i+1, len(nums)):
        # 检查i后面的数字
        if nums[j] > nums[i]:
            # 递归调用L，计算从j开始最长子序列长度。加1获得目前这个序列的总长度
            max_len = max(max_len, L(nums, j) + 1)
	return max_len

def length_of_LIS(nums):
    return max(L(nums,i) for i in range(len(nums)))

nums = [1, 5, 2, 4, 3]
print(length_of_LIS(nums))

结果

这个程序虽然能够给出正确的答案，但是最大的问题在于它的时间复杂度。假设数组的长度为n，那么就一共存在2^n个子序列，而每个子序列我们都需要去遍历一次，判断是否是递增序列。O(n*2^n)

实例1优化

我们去仔细观察上图的遍历树，会发现其实有很多重复的计算。

例如，在我们遍历子序列1，2，4的时候已经计算过“从4开始的最大子序列的长度”，后面遍历1，4的时候又重复计算了一次。

为了避免重复计算，我们可以在第一次计算的时候把结果保存下来，之后遍历到相同的节点我们就不再重复计算，直接将结果返回。这里引入字典（哈希表）。

优化代码

memo = {}

def L(nums, i)
	"""返回从第i个数字开始的最长子序列长度"""
    
    # 检查之前是否保存过这个结果
    if i in memo:
        return memo[i]
    
    if i == len(nums) - 1:
        return 1
    
    max_len = 1
    for j in range(i+1, len(nums)):
        if nums[j] > nums[i]:
            max_len = max(max_len, L(nums, j) + 1)
    
    memo[i] = max_len
	return max_len

def length_of_LIS(nums):
    return max(L(nums,i) for i in range(len(nums)))

结果

代码速度大大提升。

动态规划正是通过避免重复节点的计算，来加速整个计算过程。由于用到了字典/哈希表来保存计算的中间结果，因此也称之为“记忆化”搜索。

因为我们不需要对这些树子节点进行重复计算，所以说动态规划是“空间”换“时间”，当然也有人叫它“带备忘录”的递归，或者是递归树的剪枝。

有了递归的写法，我们也可以把它改写为非递归，或者也叫迭代的形式。从而更清晰地去分析复杂度，并且避免了递归时候的函数调用开销。

迭代

从“1”开始的最长递增序列，需要依次检查它后面的所有数。由于1可以和后面的所有数构成递增序列，所以要递归地计算从5，2，3，4开始的最长子序列长度，然后选出最长的那个，+1得到与第一个数构成的最长子序列长度。

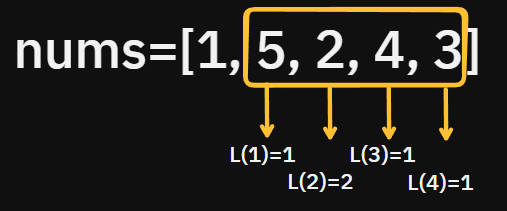
• L(0)=max{L(1)，L(2)，L(3)，L(4)}+1

同样的

• L(1)=max{L(2)，L(3)，L(4)}+1
• L(2)=max{L(3)，L(4)}+1
• L(3)=max{L(4)}+1
• L(4)=1

从后面往前一步步推，类似数学归纳法，就能把结果推算出来。最后我们根据列出来的式子来实现这个迭代算法。

def length_of_LIS(nums):
    n = len(nums)	# 5
    L = [1] * n		# 初始化数值：[1,1,1,1,1] 
    
    # 从下往上依次计算
    for i in reversed(range(n)):	# i -> 4,3,2,1,0
        # 遍历括号中的数值
        for j in range(i+1, n):
            if nums[j] > nums[i]:
                L[i] = max(L[i], L[j]+1)
	return max(L)

总结

动态规划的一般思路：

1. 穷举法/暴力搜索

   首先，我们可以简单粗暴地将所有答案穷举出来，并画出递归树，尝试写一个递归函数来求解。

2. 记忆化搜索/剪枝

   如果发现遍历中存在大量的重复计算，我们可以尝试用哈希表将数据缓存下来，之后遍历到相同的节点就直接查表，避免重复的计算。

3. 改写成迭代形式

   最后，我们可以将计算的过程表示出来，然后观察公式求解的顺序，并尝试将递归形式改写成更简洁高效的迭代形式。

参考文献

1. oiwiki，动态规划部分