如果error surface很崎岖的时候,会比较难train,能不能直接改它的land scape,让它变得比较好train呢?做Batch Normalization批次标准化对training有帮助,可以让我们在做gradient descent的时候,它的Loss可以收敛得更快,这是其中一种解决方法。
1.train里的Batch Normalization
以下是Feature Normalization的一种可能性:
  对于每一个维度i,计算他的平均值$m_i$,标准差$\sigma_i$。接下来就拿这个维度里的某一个数值,减掉这个维度的mean,除以这个维度的standard deviation,得到新的$\tilde{x_i^r}$,然后把这个新的数值$\tilde{x_i^r}$塞回去。这个$\tilde{x_i^r}$就代表有被normalize的数值。做完normalize以后,那一个维度里面的数值:均值为0,方差均为1,分布在0的上下。
  之后再重复以上操作,对每一个维度都去normalize,这样就可以得到一个比较好的error surface。
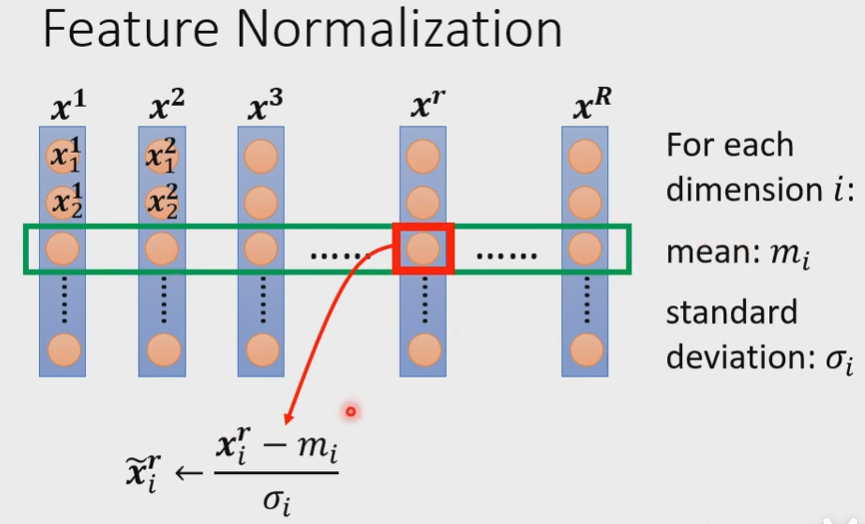
 其中$\boldsymbol{x^1\ x^2\ x^3\ …x^r…x^R}$是所有的 feature vector
  接下就把它丢到deep network里。但是$\boldsymbol{z^1,z^2,z^3}$其实也是input,虽然在前面已经做过normalization,但是通过$W^1$以后并没有做normalization,如果$\boldsymbol{z^1}$不同的dimension间数值分布仍然有很大差异,当我们要train第二层$W^2$参数的时候,就有可能很困难,所以也要对$\boldsymbol{z^1}$或者$\boldsymbol{a^1}$做Feature Normalization。
  如果$\boldsymbol{z^1}$后面的activate function是sigmoid函数,通常对$\boldsymbol{z^1}$做Feature Normalization,因为sigmoid在0附近处的斜率变化比较大。当然也可以对$\boldsymbol{a^1}$做Feature Normalization,在实际操作过程中,大家可以都试一试,比较一下两者之间的区别。
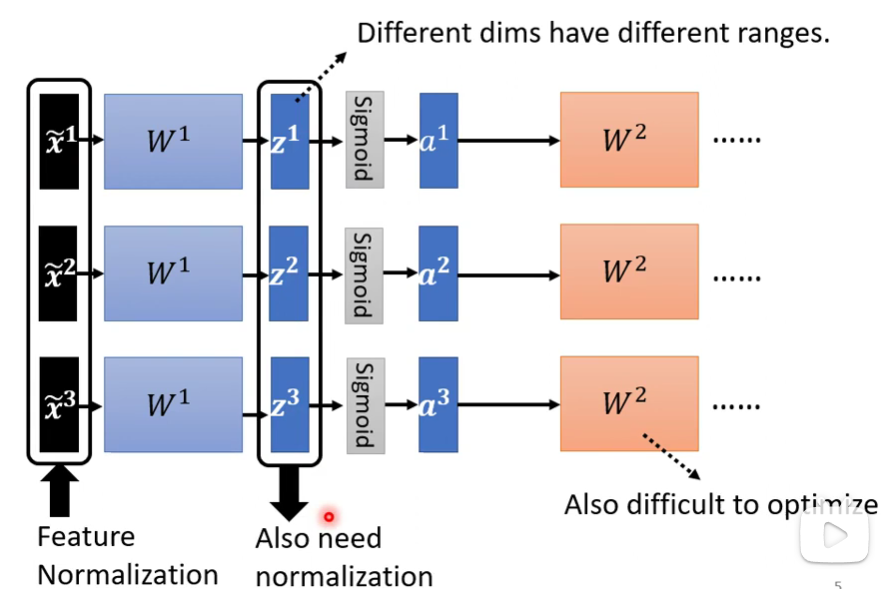
  下面举的例子是对$\boldsymbol{z^1}$做Feature Normalization。
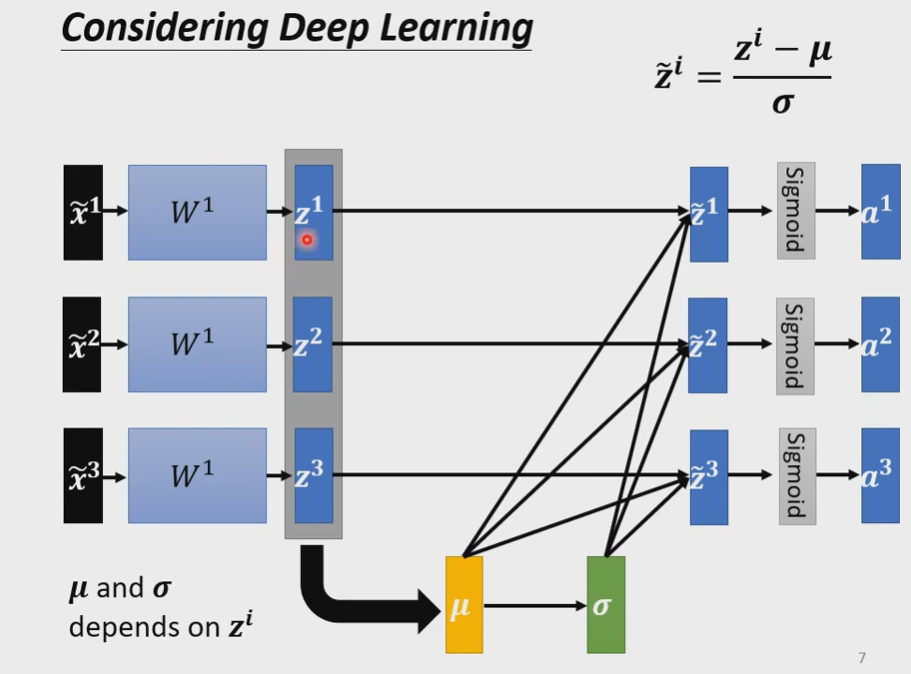
$$
\boldsymbol{\mu}=\frac{1}{3}\sum \limits_{i-1}^{3} \boldsymbol{z^i} \
\boldsymbol{\sigma}=\sqrt{\frac{1}{3} \sum \limits_{i-1}^{3} (\boldsymbol{z^i- \mu})^2}\
\boldsymbol{\tilde z^i}=\frac{\boldsymbol{z^i} - \boldsymbol\mu}{\boldsymbol\sigma}
$$
上面写的公式有点随意,大家理解了最基本的feature Normalization以后,就可以知道这三个算式在讲什么了是( ̄︶ ̄))*
  接下来,只要$\boldsymbol{z^1}$有改变,$\boldsymbol{\tilde{z^1},\tilde{z^2},\tilde{z^3},a^1,a^2,a^3}$都会有改变。就是这个network输入一堆,输出也有一堆了。
  有时候也会对$\boldsymbol{\tilde{z}}$做以下处理,因为人为的可能有比1和0更好的情况,让机器学,得出更好的error surface
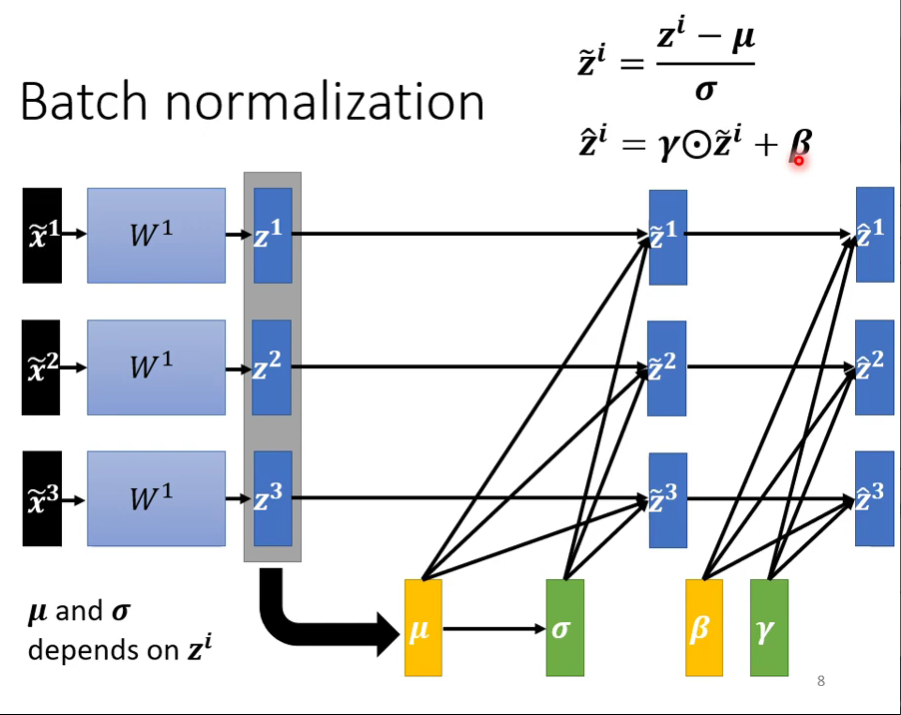
 上述的Batch Normalization都是针对training而言的,下面针对Testing来做。有时候也叫做inference
2.test里的Batch Normalization
  在进行Testing工作的时候,$\boldsymbol{\mu,\sigma}$是根据每个batch计算出来的,但是不可能总是先划分batch再验证。就比如说你是线上的工作,你设置的batch size是64,一定要等凑够64笔资料才开始normalization吗。因此通过计算在 training 时的 moving average滑动平均来替代他们,也就是每次取一个batch的时候就算一次$\boldsymbol{\mu}$,然后计算滑动平均值,$\boldsymbol{\overline{\mu} }\leftarrow p \boldsymbol{\overline{\mu}}+(1-p) \boldsymbol{\mu^t}$ 。

那么为什么做Batch Normalization会对Optimization有帮助呢?https://arxiv/abs/1805.11604