在之前的学习里面,输入的都是一个向量,例如:影像、观看人数,输出是一个数值或者一个类,那如果是其他更复杂的类别呢?输入的向量是一排,且长度可变的呢?例如:一段语音、文字、图表。在语句”I saw a saw”里面,第一个“saw”是动词,而第二个”saw”是名词,那这样机器不知道到底是输出名词还是动词了。这个时候,如果可以联系上下文,就可以推断出词义了。Self-attention自注意力机制就可以解决这种复杂的问题。
输入:
输入的是一个向量
输入的向量是一排,且长度可变
可能的输出:
- 每一个向量对应输出一个label
- 一系列向量对应输出一个label
- 由机器自己决定输出多少个label,也就是机器翻译 又叫做 seq2seq
处理的方法:
One-hot Encoding独热编码
开一个很长很长的向量,这个向量的长度和数据总长度一样。什么意思呢?假设说输入是26个英文字母,那么这个向量就是26维的,每一维对应一个字母,例如说A是[1,0,0……,0]。这个方法会有一个很明显的缺点,假如输入的数据之间是存在有关系的,如果用独热编码,那么就看不出来彼此之间的关系。
Word Embedding
它可以将文本通过一个低维向量来表达,不像one-hot那么长,语意相似的词在向量空间上也会比较相近,通用性也比较强,可以用在不同的任务中。
window滑窗
取样——量化——编码
1、Sequence Labeling:输入和输出数目一样多的向量
Self-attention会吃一整个Sequence的资讯,输入几个vector就输出几个vector
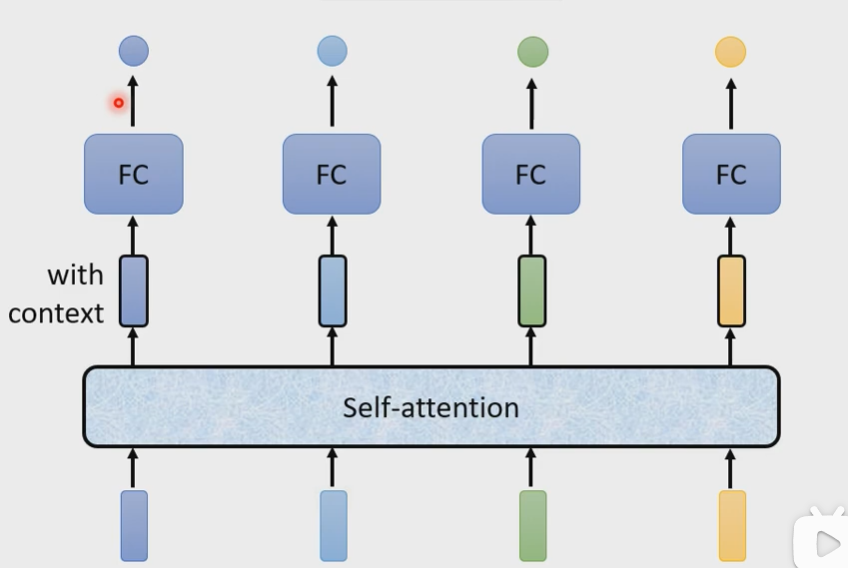
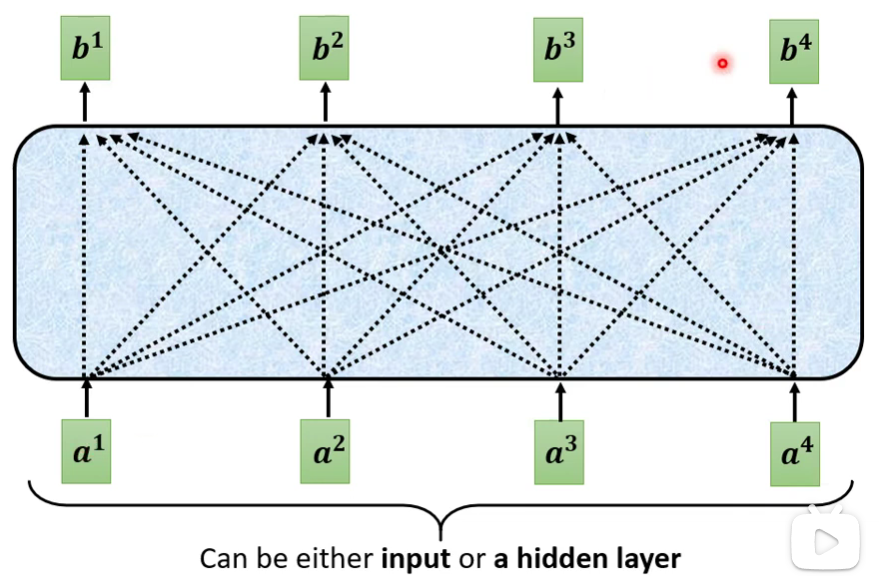 |
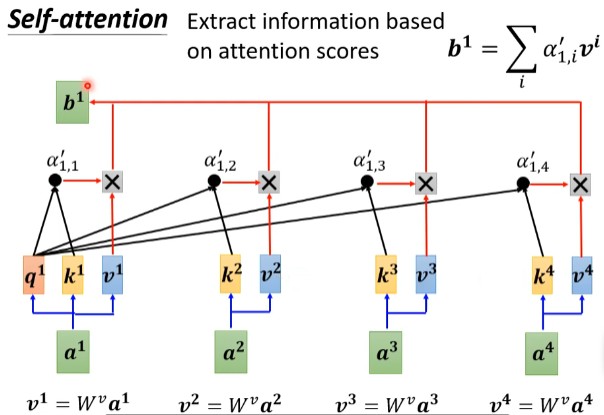 |
如上图所示,每个$\boldsymbol{b^i}$都是考虑了所有的$\boldsymbol{a^i}$产生出来的,其他每一个向量$\boldsymbol{a^j}$与$\boldsymbol{a^i}$的相关联程度用$\alpha$表示。用式子表示就是:
$$\boldsymbol{b^1}=\sum \limits_i \alpha_{1,i}’ \boldsymbol{v^i}=\sum \limits_i \alpha_{1,i}’ \boldsymbol{W^va^i}$$
计算向量之间的相关度α有以下两种方法:
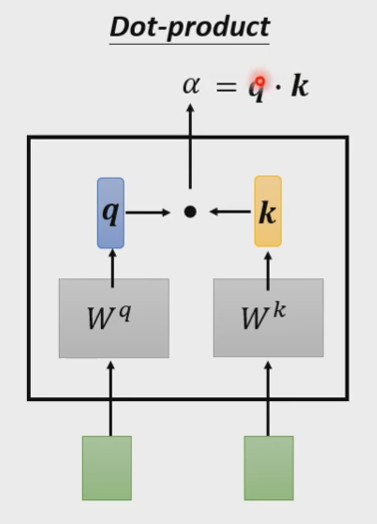 |
 |
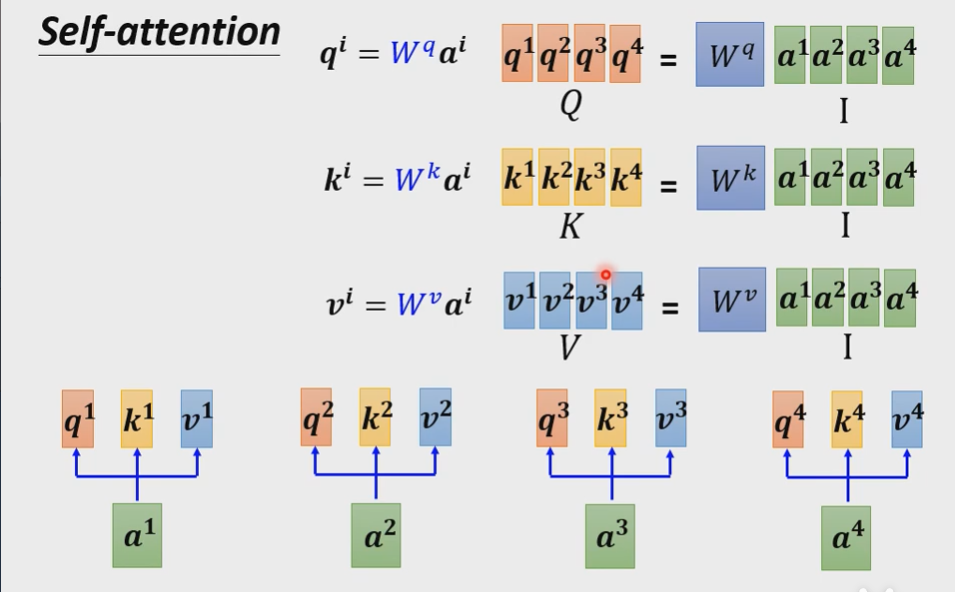
2、从矩阵乘法的角度表示Self-attention
- 从 a 得到 q, k, v
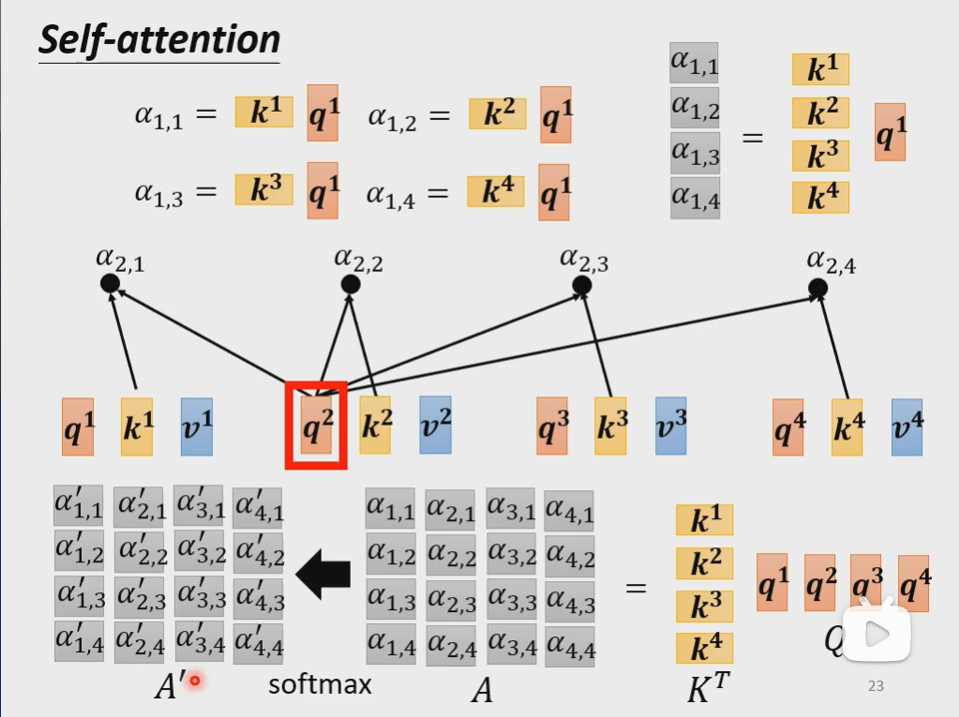
- 每一个q都去点乘k
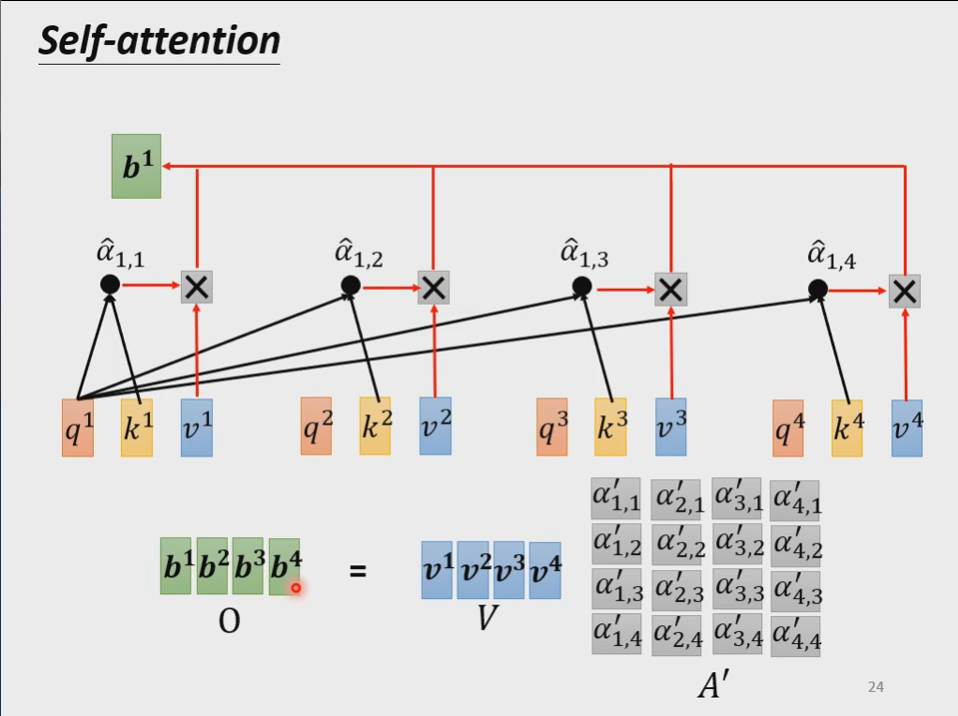
- $\alpha$乘上 v 得到 b
总结起来就是:
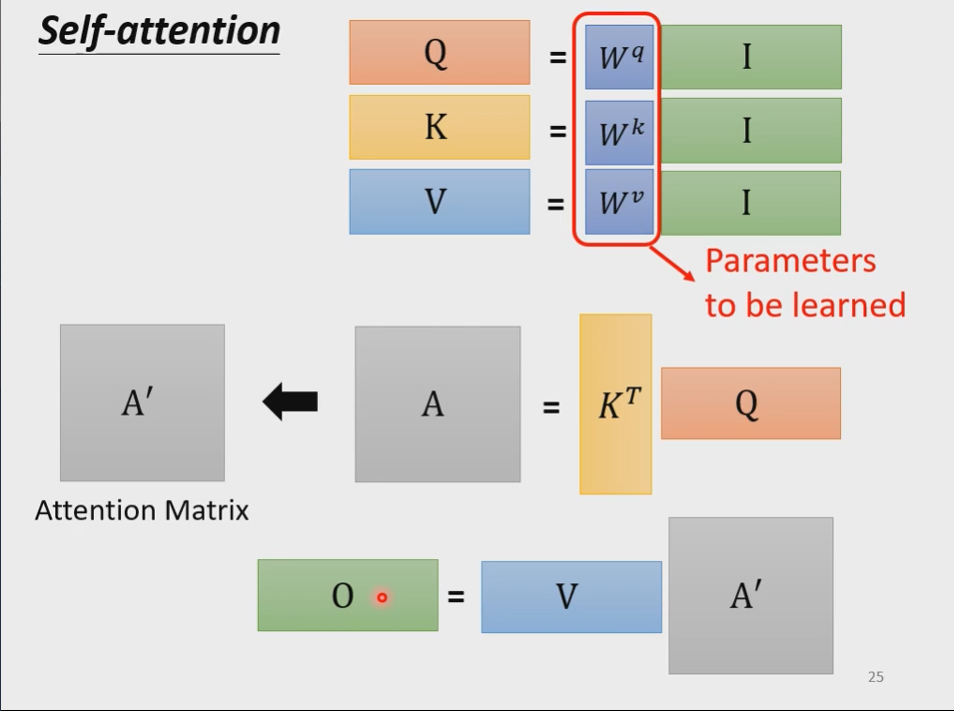
里面只有$W^q,W^k,W^v$这唯一参数是需要学习得出来的
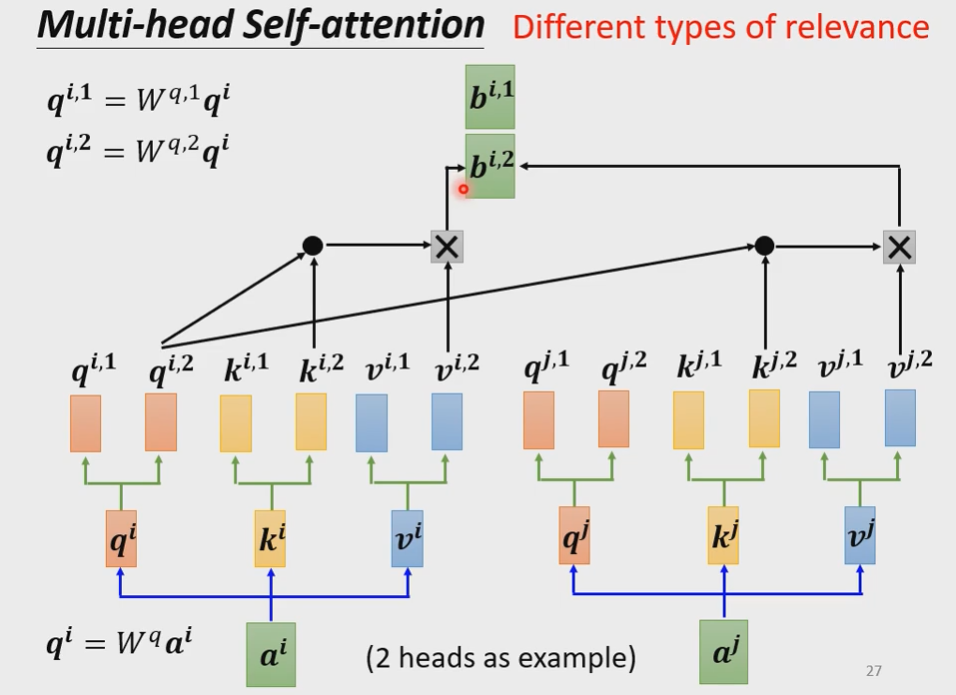
3、Multi-head Self-attention多头目自注意力机制
  在今天多头目的自注意力机制使用得更为广泛,在实际操作时,可以尝试单头目和多头目有什么不同,因为在不同的项目中,可能得得到的效果是不一样的。
 有两个不同的$W^q$,从而得出不同的$\boldsymbol{q}$。只是具体在计算$\boldsymbol{b}$时,需要把不同的$\boldsymbol{b}$拼起来,再去乘上$\boldsymbol{W^O}$。
 |
 |
4、Position Encoding位置编码
在自注意力机制里面没有位置信息。
若位置信息对于模型也有影响,那就需要为每一个位置设定一个vector,称为positional vector $e^i$
注:Position Encoding这个问题是一个尚待研究的问题,可以人为设定,也可以是机器学习得来的结果
5、CNN v.s. Self-attention
相同:CNN可以看作是一种简化版的Self-attention
不同:CNN时看的是receptive field,而做Self-attention考虑的是整张图片的信息
6、RNN v.s. Self-attention
相同:都是要处理input是sequence的情况
不同:①RNN在处理input的时候,RNN不可以并行处理,运算速度上比Self-attention慢很多;②记忆问题